04 Simetría
Junto con la periodicidad, la simetría es el principal rasgo definitorio de los cristales, como este copo de nieve, es decir, este cristal de hielo. Consiste en la invariabilidad de los cristales (de su morfología o de su estructura) con respecto a ciertas operaciones simples, como por ejemplo la rotación: Si giramos este cristal de hielo 60 grados sin que usted lo sepa, no distinguiría al volver a mirarlo que hemos realizado esa operación. Lo mismo sucederá si lo giramos 120º, 180º, 240º, 300º o, evidentemente, 360º (una vuelta completa y lo dejamos como estaba). Decimos que este cristal tiene “simetría de rotación de orden 6” o “simetría hexagonal”.

Además de la simetría de rotación existen la simetría de reflexión (como la de los espejos), de inversión en un centro, de traslación y combinaciones de ellas como los ejes helicoidales o los planos de deslizamiento.
A los cristalógrafos nos encanta la simetría. A veces hasta la obsesión. Somos unos ‘frikis’ de la simetría. Podría pensar que lo que nos atrae es la belleza de los cristales y de las estructuras cristalinas, cuya armonía está sin lugar a duda ligada a su simetría. Y efectivamente, nos gusta como les gustaba a los creadores de la Alhambra. Y les sigue gustando a los artesanos marroquíes.

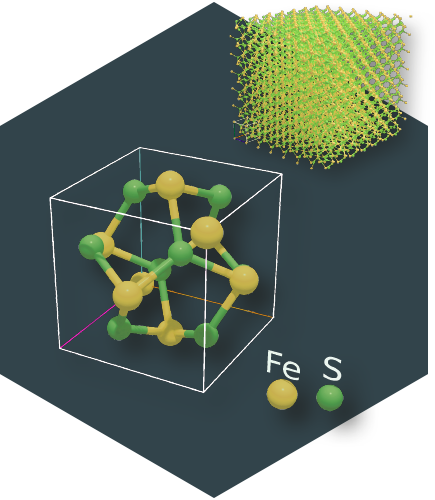
La simetría de traslación nos permite conocer la inmensa estructura cristalina estudiando solamente la configuración de sus átomos en la celda unidad. Las otras simetrías de rotación, de reflexión y de inversión reducen todavía más la representación porque parte de los átomos que hay dentro de la celda unidad son copias por simetría de otros átomos en la misma celda. La simetría nos facilita la vida a los cristalógrafos porque gracias a ella podemos clasificar y entender las estructuras cristalinas.

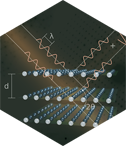
Pero sobre todo nos gusta la simetría porque simplifica enormemente el estudio de las estructuras cristalinas. Por ejemplo, la propia periodicidad deriva de una operación de simetría: la traslación. Si trasladamos la celda unidad de un cristal una distancia periódica, la estructura no cambia, es invariante. Eso nos permite representar una enorme estructura cristalina por los pocos átomos de su celda unidad, olvidándonos del casi infinito número de los otros átomos de la estructura.

Es decir, ¿de cuántas formas distintas puede ordenarse la materia? Aunque parezcan ilimitadas, lo cierto es que son muy pocas las opciones para rellenar ordenadamente un espacio repitiendo periódicamente una misma pieza.
Por ejemplo, se demuestra que solo existen cinco tipos de redes planas:
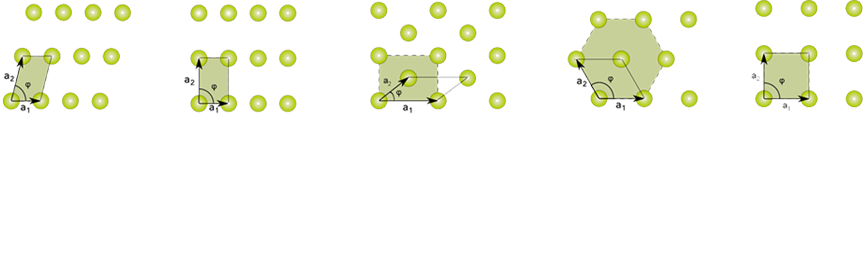
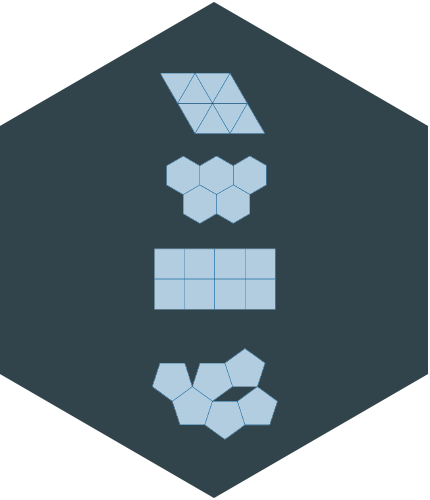
Es decir, si queremos rellenar una superficie lo podemos hacer con rectángulos, con triángulos, con cuadrados o con hexágonos, pero no con pentágonos. Y también se demuestra que en las estructuras cristalinas la simetría de rotación puede ser solamente de orden 1, 2, 3, 4 ó 6. Gracias al estudio de las combinaciones de simetría, sabemos que existen únicamente 17 formas distintas de alicatar una superficie, formas que ya eran conocidas por los geómetras árabes.

Los artesanos árabes del siglo XIII conocían los 17 grupos planos de simetría. Y también se demuestra que sólo existen 230 formas distintas de empaquetar periódicamente un volumen con unidades idénticas. Ni una más ni una menos.
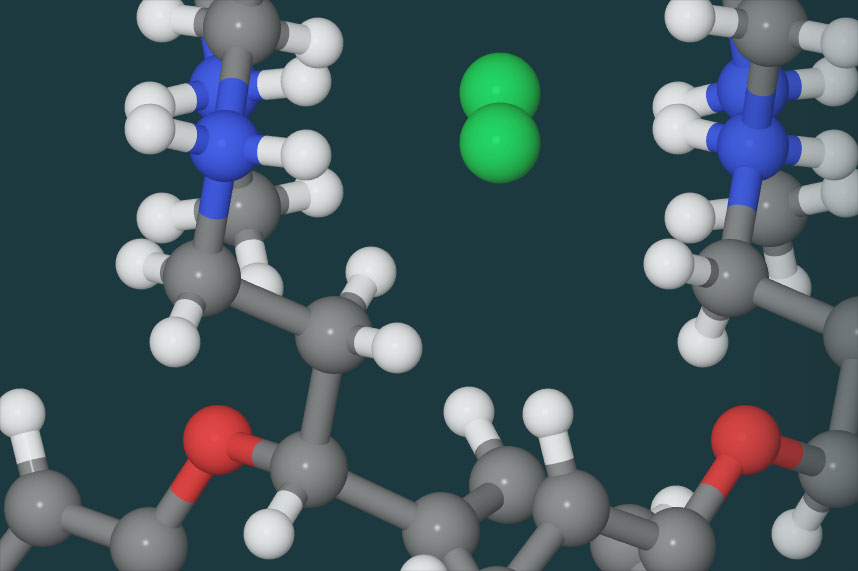

Las moléculas pueden tener simetría de rotación 5, es decir, que si se giran 72º son invariantes. Pero lo que es imposible es rellenar con ellas una superfice, hacer una red, es decir, construir un cristal. Por eso no venden losetas pentagonales en las tiendas de cerámica, o si las venden, se combinan con los rombos necesarios para rellenar los inevitables huecos entre pentágonos. Pero se ha descubierto recientemente que existen cristales con simetría de orden 5. La explicación estriba en que las superficies y los volúmenes pueden rellenarse completamente siguiendo pautas regulares pero no a la fuerza, periódicamente perfectas. Por ejemplo, pueden hacerlo con simetría de dilatación, siguiendo pautas como la serie de la proporción áurea. Es decir, materiales que están ordenados cuasi periódicamente. Son los llamados cuasicristales.
Las moléculas pueden tener simetría pentagonal. Los estructuras periódicas no pueden.