La característica que define a los cristales y los diferencia del vidrio es el orden. Los cristales son materia ordenada. Están construidos como un apilamiento ordenado de átomos o de moléculas o de conjuntos de átomos y moléculas. Siempre existe en ellos una unidad, la llamada celda unidad, que puede ser un átomo, una molécula o un conjunto de átomos o moléculas, que se repite periódicamente en el espacio rellenando un volumen.

Pero cualquier cosa ordenada de la misma manera, es decir repitiendo un mismo motivo una y otra vez siempre a la misma distancia y con el mismo arreglo es materia cristalina. Por ejemplo algo tan familiar como el enlosetado del suelo o el alicatado de las paredes. Esos ejemplos nos sirven a los cristalógrafos como modelos para explicar las propiedades de los cristales y de la materia cristalina.

Por ejemplo, el orden periódico, la periodicidad, es una de las propiedades fundamentales de un cristal. No le será difícil entender este concepto de materia periódicamente ordenada. Lo vemos en solerías, en el empapelado de las paredes o en los muros de ladrillos de las casas. Lo usamos siempre que queremos cubrir una superficie. Por ejemplo un muro de ladrillos:

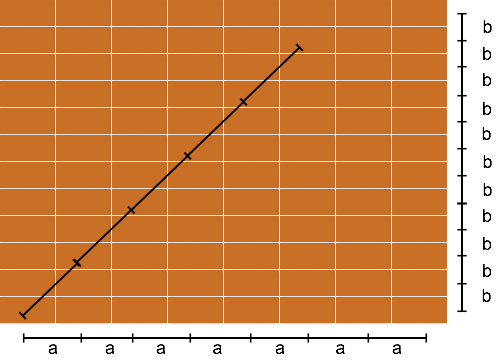
En este muro la distancia entre cada bloque o ladrillo es siempre la misma. Esa distancia se llama periodo y como puede ver cambia con la dirección. A esa propiedad de la materia así ordenada se le llama periodicidad. Así de fácil.

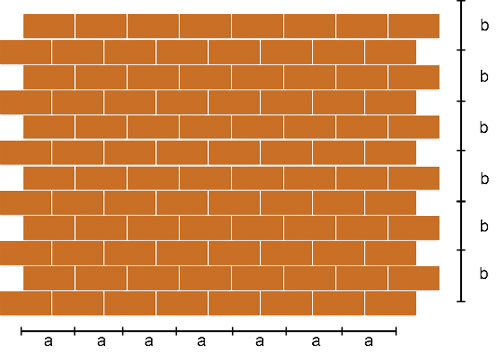
En este otro arreglo, que se conoce como al tresbolillo, también los ladrillos están colocados a una distancia idéntica pero el valor de los periodos cambia. La estructura es diferente pero también periódica, es decir también cristalina

Esos ladrillos son el equivalente a lo que llamamos celda unidad cristalográfica. Para crear una estructura cristalina solo tiene que imaginarse convertir esos ladrillos en unidades moleculares. Le vamos a ayudar a imaginar cómo hacerlo convirtiendo cada ladrillo cúbico de un juego de construcción por la unidad repetitiva de un cristal molecular.

La celda unidad que hemos elegido es la de la pirita, un sulfuro de hierro muy común, un mineral muy bonito de color dorado.

Si colocamos bloques o celdillas uno junto a otro formando una fila tendremos una distribución periódica en una dirección:

Si empaquetamos varias de estas filas en la dirección perpendicular tendremos un plano periódico en dos direcciones. Esto es un cristal bidimensional:

Finalmente, si apilamos bloques o celdillas unidad en la tercera dirección, tendremos un apilamiento tridimensional periódico de elementos idénticos.

Esto es un cristal. La única diferencia es que un cristal de un centímetro de pirita contiene alrededor de 100000000000000000000000 celdillas unidad en vez de las trescientas cuarenta y tres de la ilustración.

Cristales de pirita

Ahora, imagínese que se encuentra en el interior de esa estructura cristalina. Colóquese en un átomo de hierro y mire su entorno. Muévase al mismo átomo de hierro de otra celda y era que su entorno es el mismo. Esa es otra propiedad de los cristales: la homogeneidad. Lo puede hacer en nuestra colosal instalación de la estructura cristalina:

Ahora trate de desplazarse en una dirección determinada. Tendrá que sortear con dificultades los enlaces que unen a los átomos. Párese y cambie la dirección de movimiento. Verá que la dificultad de moverse ha cambiado también. Esa es otra propiedad importantísima de los cristales: la anisotropía.

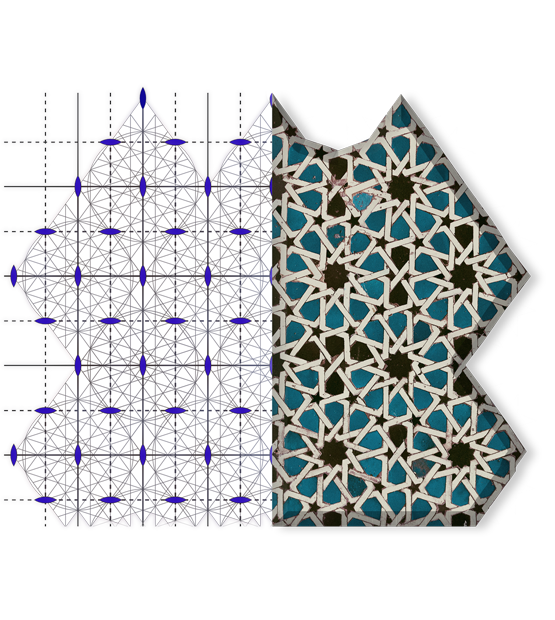
Los cristalógrafos hemos logrado desvelar todas las distintas maneras de agrupar elementos periódicamente. Hay 17 formas de hacerlo en una superficie y 240 de hacerlo en tres dimensiones. Los geómetras árabes exploraron de forma especialmente brillante las superficies periódicas. Bellísimos ejemplos se pueden lograr en la Alhambra de Granada o en el Alcázar de Sevilla.

Y aun hoy día se realizan y buscan nuevos diseños en el reino de Marruecos.

Usted podrá hacerlo en nuestra instalación de mosaicos.

¿Sabías que…?

• No existen dos copos de nieve iguales ya que el crecimiento de cada cristal de hielo depende de múltiples factores.
• Fedorov demostró en 1891 que no hay más de 17 estructuras básicas para las infinitas decoraciones posibles del plano formado mosaicos periódicos.
• La simetría es un concepto que sustenta muchas cosas: en biología, por ejemplo, el virus H1N1 es un objeto simétrico y usa la simetría para replicarse.
• Los azulejos de la Alhambra están dispuestos en tramas y repeticiones obsesivas, se rigen por una estricta serie de esquemas simétricos, de forma que si se giran, conservan la misma apariencia (algo parecido a rotar un triángulo equilátero), lo que quizá explique algo de su magnetismo.

Para saber más…

• La pagina web de Wikipedia sobre simetría es la mejor fuente para empezar a conocer más sobre los diferentes tipos de simetría y su relación con otras disciplinas científicas.
• También puedes visitar la página sobre geometrías en la naturaleza y aprender como identificar formas geométricas en la naturaleza.
• En la página wikipedia sobre fractales encontrarás información muy interesante acerca de la geometría en el mundo natural.